
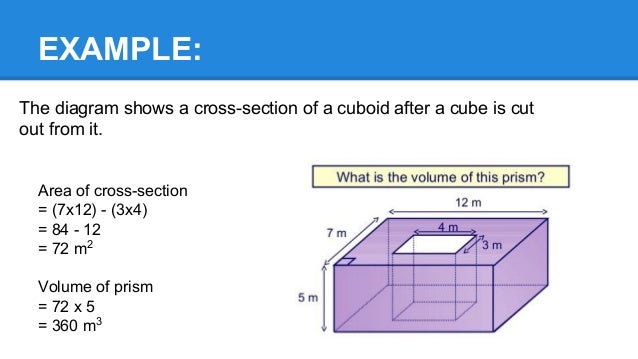
Where the holes are arrayedin an orthogonal grid, as shown in Figure 1.53 a, the failure surface is easily determined.
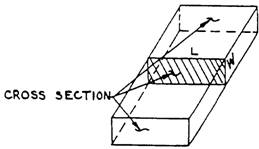
Failure or "rupture" of an element stressed in tension occursat a failure surface defined by the location and quantity of such bolt holes. Where bolt holes reduce the cross-sectional area of a tension element, the remaining area at thecross section, A n, is called the net area. The plastic section modulus for a rectangular cross section can be determined by multiplying each section half (e.g., the shaded area shown in Figure 1.51) by the distance from its centroid to the centroid for the whole section: Z x = B( H/2)( H/4) + B( H/2)( H/4) = B H 2/4.įigure 1.52: Illustrations of (a) tension element and (b) free-body diagram cut at any cross-section with area, A Rather, it is defined as the sum of all elemental areas above or below the centroid ( x-axis) of the cross section multiplied by the distance from each of the individual elemental centroids to the centroid of the cross section as a whole. Unlike the elastic section modulus, S x, the plastic section modulus has no fixed relationship to the moment of inertia of the cross section. This property is unique to steel, since neither of the other materials we are considering (wood and reinforced concrete) has the necessary ductility to reach this state. The plastic section modulus, Z x, is used to determine the limit state of steel beams, defined as the point when the entire cross section has yielded. From Equations 1.8 and 1.11, it can be seen that the section modulus for a rectangular cross section is S x = ( BH 3/12)/( H/2) = BH 2/6. In each case, the moment of inertia is divided by half the cross-sectional height, or thickness. What may not be as immediately clear is that the -shaped cross section (Figure 1.49 b) has an area, A = ( B × H) – ( b × h), and the circular ring (Figure 1.49 d) has an area, A = π R 2 – π r 2, where R is the outer and r is the inner radius.įor the circular shapes, S x = I x/ R (Figures 1.49 c and 1.49 d). AreaĬross-sectional areas are easily determined: for rectangles, the area A = B × H (Figure 1.49 a) and for circles, A = π R 2 (Figure 1.49 c). What follows is a brief overview and summary ofthe major cross-section properties encountered in structural analysis and design, followed by a discussionof tension, compression, and bending. Instead, the load or moment that anelement can safely resist can only be determined when information about the element's cross sectionand material properties is considered: clearly, a large cross section is stronger than a small one.But "large" in what way? The cross-sectional properties relevant to the determination of structuralsafety and serviceability are different for tension elements, columns, and beams and are, therefore,discussed more fully in their appropriate context.

The magnitude of internal forces and bending moments do not, by themselves, give any indicationas to whether a particular structural element is safe or unsafe. 1 Appendix Chapter 1 – Introduction to structural design: Strength of materials Introduction to structural design | Statics | Tributary areas | Equilibrium | Reactions | Internal forces | Indeterminate structure | Material properties | Strength of materials | Sectional properties | Construction systems | Connections | Ch.


 0 kommentar(er)
0 kommentar(er)
